磁场中的高斯定理
-
磁通量:。通过磁场中某一曲面的磁感应线条数。
磁通量的正负与电通量的正负同理,穿出曲面为正,穿入曲面为负。
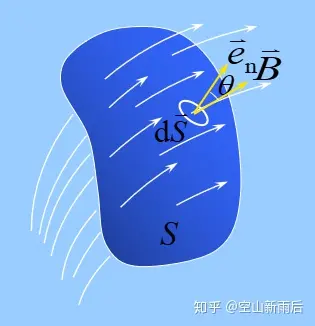
- 磁场中的高斯定理: ,在磁场中通过任意闭合曲面的磁感应强度通量等于零。这说明了磁场是无源场,磁感线连接成了一个闭环。(不同于我们前面说的电场是有源场,由电荷作为起点或则终点)
安培环路定理
-
安培环路定理:。在恒定电流的磁场中,磁感应强度沿任何闭合路径一周的线积分(即环路积分),等于闭合路径内所包围并穿过的电流的代数和的 倍,而与路径的形状大小无关。 这个定理说明了磁场是有旋场,非保守力场。(这个定理需要细细品一下,可能看着例题想这个定理会简单一下。实际上就是磁场与电场的高斯定理与安培(静电)环路定理的地位反过来了,在电场的计算里面高斯定理尤为重要,而在磁场的计算里面,安培环路定理尤为重要)
-
- 安培环路定理的正负:对于单个电流,大拇指指向电流方向,若积分路径与四指旋转的方向相同就为正,反之为负。
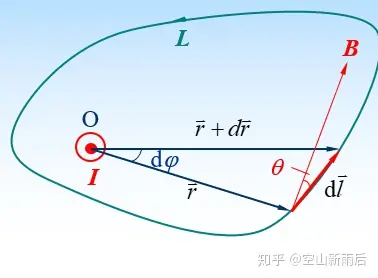
(以这个图为例,电流I穿出纸面向外,这时候把你的大拇指指向你自己(我想应该每个人都是对着手机或则电脑的吧),这时你的大拇指指向就是电流的方向。你看你的四指是弯曲向逆时针方向的,如图积分路径L的绕向也是逆时针方向,那么这个就是正值。)
- **当电流并不是垂直于积分路径所在平面的时候:**将电流正交分解到垂直于积分路径所在平面和积分路径所在平面内的两个方向的电流,再用垂直于积分路径所在平面的电流进行计算。
- **使用条件:**只适用于真空中的恒定电流产生的磁场。
- 与电场的对比:

例题
1.求无限长圆柱形载流导体的磁场,圆柱形载流导体有均匀的恒定电流,电流方向垂直于纸面向外。
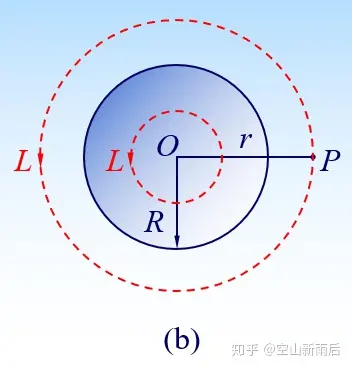
解:先取一个半径为的圆形积分回路,那么根据安培环流定理可知。
。这就得到了圆柱外面的磁场强度。
再取一个导线内的半径为的圆形积分回路
。这就得到了圆柱内部的磁场强度。
最后就可以得到如下的图形 。
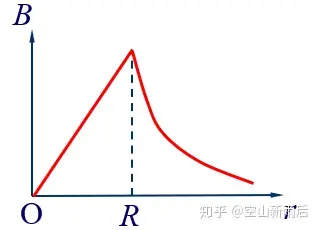
2.长直螺线管内的磁感应强度。
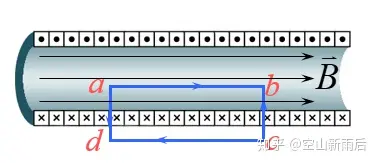
解:
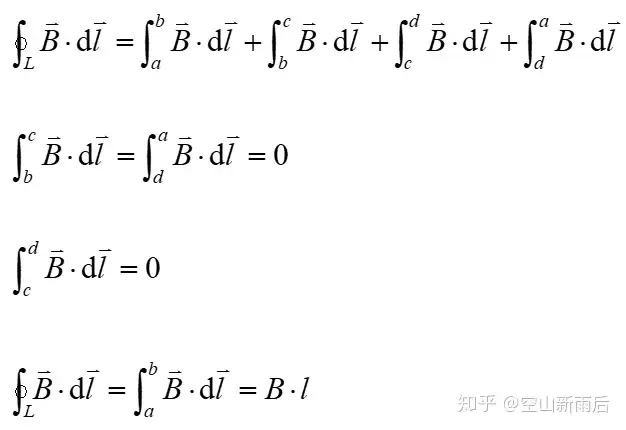

- 无限长载流螺线管的磁场
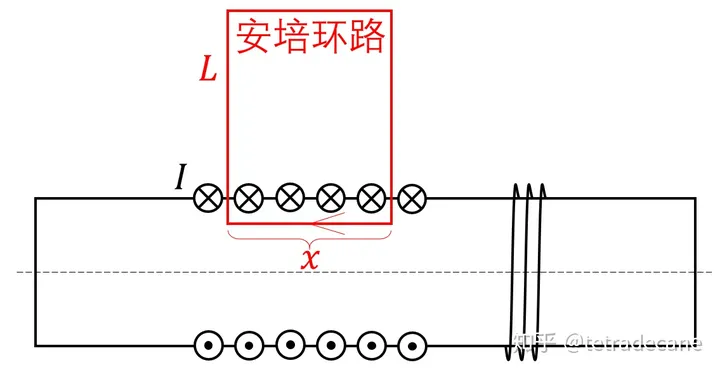
图2 无限长载流螺线管的磁场
设无限长载流螺线管均匀密绕,单位长度上导线的匝数为 ,电流恒为 .
取如图所示的安培环路 ,左右两条边的磁环量根据对称性显然为零,上面一条边若离得足够远也能使磁环量为零,则回路的磁环量完全由下面一条边决定,而且该边上的 应为恒定值。由磁场环路定理得